Docs version here: http://ow.ly/tPuO0
How to Determine the Distance to the Horizon - For Dummies
Well, let’s check whether the above is true or not. In this article I will present two experiments that you can conduct to see what the real shape of Earth is. The first one is based on optical zooming, so basically all you need is a good camera or camcorder. For the second one you would need a..laser, strong enough to let the beam travel a couple of kilometres. The Polish guy, Mariusz Szczytynski, who is the author of Polish ‘Skycentrism’ movies that I translate, made the first one. Who has a good laser can try the second one as well.
The other goal except for checking the curvature of Earth was to tell whether the experiment conducted in Neapol in 1897 by Cyrus Teed and his crew was valid or not. You can watch how this experiment was made here:Skycentrism: We live inside the Earth, part II - Geodesy (English subtitles, napisy ENG) - YouTube (captions)
The aim of it was to measure the surface of the ocean, whether it’s convex or concave. The results were inconvenient for the official science and none has repeated it since then. Even though it should be much easier to perform nowadays with all technology that we have. It would be really easy to show that this historical experiment was conducted in a wrong way and its results were false.
Fortunately it turns out that this can be in fact checked and repeated by..everyone.
The experiment made by Mariusz was conducted on Turawa Lake in Poland. He used JVC Everio camcorder with 40x optical zoom. Its elevation was 50 cm above the water surface. The lower you can place your device the better. Take a look at this picture now:
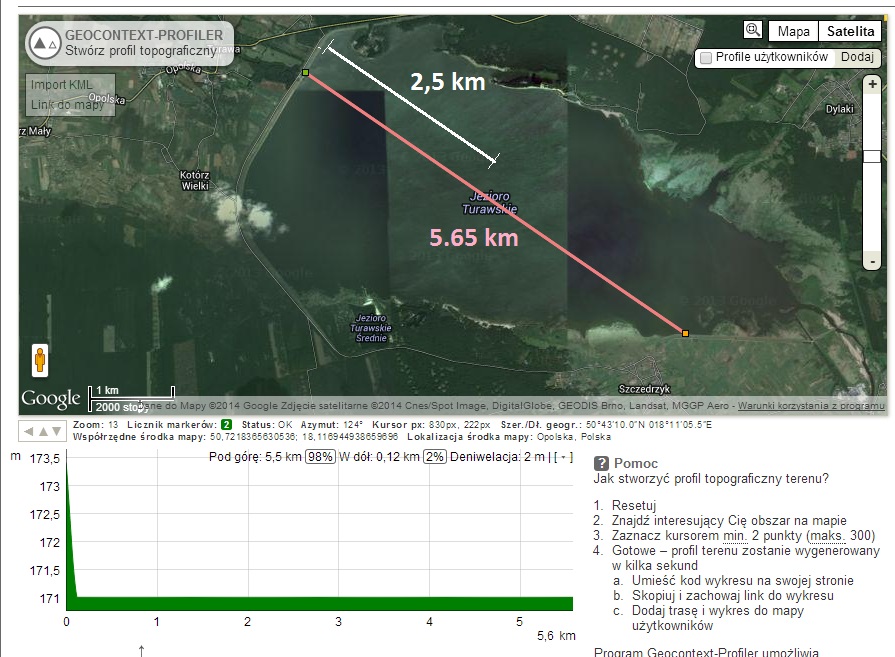
Conditions while taking the pictures:
white segment - calculable maximum visibility range for the height of 50 cm:
Where R is the radius of Earth (6371 km) including elevation of Turawa Lake above sea level (171 m), h is the height of the camera (0,0005 km)
d= 2,5 km. This is how far we should be able to see from 50 cm on a convex Earth. We have no right to see further than that.
pink segment - distance to the opposing shore: 5,65 km.
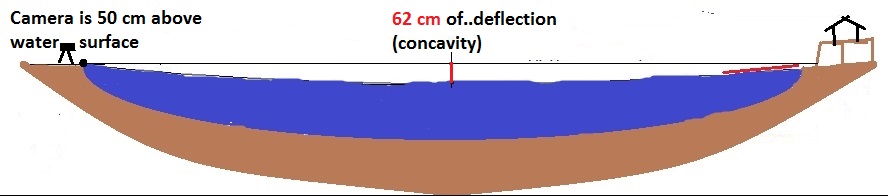
Calculable convexity for the distance of 5,65 km is 62 cm. This means that there is supposedly a 62 cm bulge in the middle of the lake.
Google Translate
Now, let’s go for the photos that were made.
Above could in fact end the subject. This was made by a camera placed 50 cm above the water surface. It is also below the calculable convexity which is 62 cm. The camera is 12 cm below the supposed convexity that should block the view.
What can we see here ? A mirror image of the building as well as the shoreline on..the water surface. There is no way the see the reflection of the shoreline if the lake was..convex.
Another photo:
This small building is on the left from the one in the previous picture. We see the reflection of it in the water as well. Also notice the path on the right. The part that curves the other way is..a reflection. What also grabs our attention is a..duck near the shore to the left of the building.
Here we can see that the conditions changed a bit and the reflection disappeared.
This scheme shows why we could see the reflection of the shore and buildings on the water:
And here’s an official version.
Below is a proposition of the laser experiment.
Above could be done on a lake, bay or any other water reservoir. For 7km for example, the calculable convexity is 98 cm. On one side we place the laser on the height of let’s say 20 cm. On the other shore we put a reader/mirror or something that the laser beam would hit on the height of 20 cm as well.
If we live on the convex Earth, the laser beam will never reach the reader on the other side. It will..hit the water instead.
The final question now is: if you try one of these two experiments and get similar results, what will you do with it ?
Skycentrism movies: ka rol - YouTube
Is the Earth convex or concave ? Do it yourself !
The Earth curves faster than most people think. On a small lake — say, 2.5 miles across — there’s a 1-foot-tall bulge in the middle of the lake due to the curvature of the Earth. On some larger bodies of water, if conditions are right, you can actually perceive the curvature of the Earth when this sort of bulge blocks your view of the opposing shore.How to Determine the Distance to the Horizon - For Dummies
Well, let’s check whether the above is true or not. In this article I will present two experiments that you can conduct to see what the real shape of Earth is. The first one is based on optical zooming, so basically all you need is a good camera or camcorder. For the second one you would need a..laser, strong enough to let the beam travel a couple of kilometres. The Polish guy, Mariusz Szczytynski, who is the author of Polish ‘Skycentrism’ movies that I translate, made the first one. Who has a good laser can try the second one as well.
The other goal except for checking the curvature of Earth was to tell whether the experiment conducted in Neapol in 1897 by Cyrus Teed and his crew was valid or not. You can watch how this experiment was made here:Skycentrism: We live inside the Earth, part II - Geodesy (English subtitles, napisy ENG) - YouTube (captions)
The aim of it was to measure the surface of the ocean, whether it’s convex or concave. The results were inconvenient for the official science and none has repeated it since then. Even though it should be much easier to perform nowadays with all technology that we have. It would be really easy to show that this historical experiment was conducted in a wrong way and its results were false.
Fortunately it turns out that this can be in fact checked and repeated by..everyone.
The experiment made by Mariusz was conducted on Turawa Lake in Poland. He used JVC Everio camcorder with 40x optical zoom. Its elevation was 50 cm above the water surface. The lower you can place your device the better. Take a look at this picture now:
Conditions while taking the pictures:
- Sunny, hot weather and no wind.
- Very good visibility.
- Pictures taken 4 hours before sunset.
white segment - calculable maximum visibility range for the height of 50 cm:
Where R is the radius of Earth (6371 km) including elevation of Turawa Lake above sea level (171 m), h is the height of the camera (0,0005 km)
d= 2,5 km. This is how far we should be able to see from 50 cm on a convex Earth. We have no right to see further than that.
pink segment - distance to the opposing shore: 5,65 km.
Calculable convexity for the distance of 5,65 km is 62 cm. This means that there is supposedly a 62 cm bulge in the middle of the lake.
Google Translate
Now, let’s go for the photos that were made.
Above could in fact end the subject. This was made by a camera placed 50 cm above the water surface. It is also below the calculable convexity which is 62 cm. The camera is 12 cm below the supposed convexity that should block the view.
What can we see here ? A mirror image of the building as well as the shoreline on..the water surface. There is no way the see the reflection of the shoreline if the lake was..convex.
Another photo:
This small building is on the left from the one in the previous picture. We see the reflection of it in the water as well. Also notice the path on the right. The part that curves the other way is..a reflection. What also grabs our attention is a..duck near the shore to the left of the building.
Here we can see that the conditions changed a bit and the reflection disappeared.
This scheme shows why we could see the reflection of the shore and buildings on the water:
And here’s an official version.
Below is a proposition of the laser experiment.
If we live on the convex Earth, the laser beam will never reach the reader on the other side. It will..hit the water instead.
The final question now is: if you try one of these two experiments and get similar results, what will you do with it ?
Skycentrism movies: ka rol - YouTube
Last edited:
